|
El álgebra trata con números y las operaciones
entre éstos. Su cualidad principal que la distingue de
la aritmética es el uso de letras para representar números.
A las letras que representan números se les llama literales
numéricas o simplemente literales.
En general en el álgebra las letras se usan como variables por
que ellas pueden representar diferentes números y los
números se denominan constantes.
Considérese ahora que a y b representan
números, su producto se escribe usualmente así: ab,
sin el signo de multiplicación, aunque también
se puede escribir como: a × b o a · b.
Por ejemplo, para 5 y la literal numérica c,
su producto de se escribe usualmente así: 5c
Las operaciones fundamentales del álgebra son suma, resta
o sustracción, multiplicación y división
o cociente.
Propiedades Generales Básicas. Algunas
propiedades básicas que siempre se deben de tener presente
son:
La suma de dos números es la misma cualquiera
que sea el orden en que se sumen
|
PG1 |
La suma de tres o más números es la misma
cualquiera que sea la forma en que se agrupen:
a + b + c = (a
+ b) + c = a + (b + c) = (a + c) + b
|
|
PG2 |
El producto de dos números es
el mismo cualquiera que sea el orden en que se multipliquen:
|
PG3 |
El producto de tres o más números
es el mismo cualquiera que sea la forma en que se agrupen:
abc
= (ab)c = a(bc) = (ac)b
|
|
PG4 |
| El producto de un número por la suma de otros números
es el mismo que la suma de los resultados de multiplicar
cada uno de los otros números por el primero (Ley
distributiva):
|
PG5 |
Cantidades iguales a una misma cantidad son iguales entre
ellas.
a
= c y b
= c,
entonces a = b
|
|
PG6 |
Si cantidades iguales son sumadas a cantidades
iguales, las sumas serán iguales:
a
= b, entonces a + c =
b + c
|
|
PG7 |
Si cantidades iguales son restadas de cantidades iguales,
los resultados serán iguales:
a
= b, entonces a
- c =
b - c
|
|
PG8 |
Si cantidades iguales son divididas por cantidades iguales
diferentes de cero, los cocientes serán iguales:
a
= b, entonces a ÷ c =
b ÷c,
con c 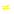 0 0
|
|
PG9 |
Una cantidad puede ser substituida por
su igual en expresiones algebraicas.
|
PG10 |
Sobre los números negativos Es necesario revisar este tema, al final de este párrafo
hay una liga que conduce a él.
Se recomienda estudiar a detalle el mapa conceptual
los
enteros. Estudiar todo el tema, después
regresar a esta página, basta cerrar la ventana
del tema de enteros.
A
los números negativos
| 2. Expresiones algebraicas |
|
Las expresiones algebraicas están formadas por variables,
constantes, signos de agrupación
y operaciones como suma, resta, multiplicación, división,
elevación a potencia o extracción de raíz.
La siguiente es una expresión algebraica.
En este acaso la expresión está formada por cuatro
términos. Cuando una expresión está compuesta
de partes conectadas por los signos + o - , entonces a cada una
de las partes tomada con el signo que le precede (si no hay signo
precediendo se le asigna el signo +) se le llama término,
término de la expresión algebraica.
Un término puede ser un número o una variable,
o un producto o un cociente de números y variables, o
la raíz
o potencia de estos productos o cocientes, como los del ejemplo
anterior.
Cuando un término se forma por la multiplicación
de sus partes, una de éstas o cualquier producto de ellas
se llama factor del término.
Para el término 7abc,
algunos factores son: 7, a, b, c, 7a, 7b, ab,
abc, etc.
Factor
|
Se puede expresar así
|
7
|
7abc = 7(abc)
|
a
|
7abc = a(7bc)
|
7a
|
7abc = 7a(bc)
|
ab
|
7abc = ab(7c)
|
etc.
|
etc.
|
|
Cualquier factor de un término se llama coeficiente del
resto. El coeficiente de la parte literal de un término
se llama coeficiente numérico.
En el caso anterior 7a es el coeficiente
de bc y 7 es
el coeficiente numérico del término.
En la expresión - 9xy, el coeficiente
numérico es - 9.
En el caso de la expresión formada por la única literal t,
el coeficiente numérico es 1.
Para el caso del término - n,
el coeficiente numérico es - 1.
2.1 Evaluación de expresiones
algebraicas
Calcular el valor de 4a2 + 2a - 3,
cuando a = - 2
Procedimiento de evaluación:
se substituye en la expresión el valor de a y
se simplifica la expresión numérica resultante.
Hay que tener cuidando de aplicar correctamente las propiedades
sobre la jerarquía de las operaciones.
(Si lo requieres puedes revisar el tema: A
la jerarquía de las operaciones).
Evaluación: Si a
= -2, entonces:
4a2 + 2a - 3
= 4(-2)2 + 2(- 2) - 3 = 4(4) - 4 - 3
= 16 - 7 = 9
Entonces el valor de la expresión para a
= -2 es 9
|
Calcular el valor de la expresión: (v
+ m)v - (v - m)m, si v = 7, m = -3.
(v + m)v
- (v - m)m
= (7 + (- 3))7
- (7 - (- 3))(-
3) = (4)7
- (10)(-3)
= 28 - (- 30) = 58
Por lo tanto para v = 7 y m = - 3,
la expresión vale: 58
|
Las fórmulas son expresiones matemáticas
conocidas por todos nosotros y no son de uso exclusivo de la
matemática. Fórmulas se encuentran en casi todos
los campos del conocimiento. Son expresiones que relacionan
varias variables.
Por ejemplo en matemáticas algunas fórmulas
para calcular perímetros, áreas y volúmenes
son:.
| Cualidad medida |
Fórmula
|
| Perímetro del rectángulo |
P
= 2(a + l)
|
| Volumen del cubo |
V
= l³
|
| Área del triángulo |
A
= ½(b × a)
|
| Superficie de la esfera |
S
= 4 × ¶ × r²
|
| Perímetro del círculo |
P
= ¶ × 2 r
|
Ejemplos de física:
| Segunda ley de Newton (Mecánica) |
F
= m × a |
| Fuerza de atracción gravitatoria (Mecánica) |
F
= G(m1×m2 /
r²) |
| Ley de Hom (Electricidad) |
I
= V / R |
| Ley de Boyle (Cinética de gases) |
C
= pV |
| Ley de los cuadrados inversos (Fotometría) |
E
= I / D² |
Cálculo con fórmulas:
1. Calcular el área de un rectángulo
si su ancho (a) es 3 metros y su largo 5 metros:
Fórmula: A
= a × l, donde A representa
el área del rectángulo, a la
medida del ancho y l la
medida de su largo.
Cálculo: A =
3 mts × 5
mts = 15 mts
2. Si cuerpo que se mueve siempre con la misma
velocidad, la siguiente fórmula relaciona la velocidad
(v) con la distancia (d) que viaja el cuerpo y el tiempo (t)
de duración del viaje.
v
= d / t
Si d =
120 kilómetros y t =
5 horas, calcular la velocidad con la que se mueve el cuerpo.
Solución: v =
120 kilómetros / 5 horas = 24 kilómetros / hora
En este tablero Descartes las letras p y q son
variables, representan números, p la
longitud del segmento azul y q la
del segmento rojo. El área del rectángulo
modela su producto p × q.
Para ver mejor lo que ocurre, seleccionar "si" en
el cuadro de opciones de valores en
lugar de "no" que
aparece ya seleccionada.
Variar los valores para observar lo que ocurre. Usar
el botón Inicio para volver a
empezar.
|
|
|
| Lo interesante
es experimentar el concepto de variable, su carácter
numérico y su variabilidad. Copiar
la tabla en el cuaderno y llenarla con valores que
da el tablero cuando se hace variar tanto p como q. |
p
|
q
|
p × q
|
1.5
|
2
|
|
2.8
|
|
9.8
|
|
|
2.5
|
5
|
3.5
|
1.5
|
|
1.8
|
|
6.3
|
2.5
|
3.5
|
|
|
|
3.1. Términos semejantes
Se llaman términos semejantes a aquellos
que ser forman por la multiplicación de las mismas
literales con los mismos exponentes (para el concepto de exponente
ver
el mapa
conceptual
para los números enteros):
Son términos semejantes
|
No son términos semejantes
|
10a, 3a
|
10a, 3b
|
-5a2,11a2
|
-5a2, 11a
|
-x, x
|
-1, x
|
6abcd, -abcd
|
6abcd, -abct
|
3e2n3, 9e2n3
|
5e2n3, 5e4n
|
½ xyz, ¼ zyx
|
¾ xyz, ¾ xya
|
3.2. Una propiedad importante en álgebra es la Ley
distributiva
El producto de un
número por la suma de otros números es el
mismo que la suma de los resultados de multiplicar cada
uno de los otros números por el primero.
|
Para los siguientes ejemplos posiblemente requieras revisar
la operatividad de números
con signo, la siguiente liga conduce al tema: A
los números negativos
Aplicación de la ley distributiva:
6(2x + 7y) = 6 · 2x
+ 6 · 7y = 12x + 42y
Finalmente resulta: 6(2x + 7y) = 12x + 42y
-4(11a + 5c) = -4 · 11a
+ (-4) · 5c = -44a - 20c
Resultando: -4(11a + 5c) = -44a - 20c
6c(2p - 5s) = 6c · 2p
- 6c · 5s = 12cp - 30cs
Por lo tanto: 6c(2p - 5s) = 12cp - 30cs
x(2y - 3z + 4w) = x · 2y
- x · 3z + x · 4w
= 2xy - 3xz + 4xw
Finalmente: x(2y - 3z + 4w) = 2xy - 3xz + 4xw
En todos los casos es claro como el primer factor de la expresión
inicial se distribuye, respetando las reglas de los signos, sobre
los sumandos del segundo factor.
3.3. Reducción de términos semejantes
Cuando se suman o se restan términos semejantes se dice
que se reducen. Para sumar o restar términos semejantes
se suman o se restan sus coeficientes numéricos lo que
da el coeficiente del resultado que es un término semejante
a los que se redujeron, así:
10a + 3a = (10 + 3)a = 13a
(Notar que se aplica la ley distributiva en sentido contrario)
7s²p³ - 2s²p³ = (7 - 2)s²p³ =
5s²p³
-3abc - 3abc = (-3 - 3)abc = -6abc
Si una expresión algebraica contiene términos
en los cuales algunos son semejantes y otros no lo son, la expresión
puede simplificarse reduciendo los que sí son semejantes.
Por ejemplo:
Simplificar: 5a + 3 c + 2a - 6a +
7c
Procedimiento:
5a + 3 c + 2a - 6a +
7c = (5 + 2 - 6)a + (3 +7)c
= 1a + 10 c
Se hace así por que el primero, tercero y cuarto
términos son semejantes, lo mismo ocurre con el segundo
y último términos, entonces lo que se hizo fue
reducirlos por separado.
Finalmente, la simplificación queda así:
5a + 3 c + 2a - 6a + 7c = a + 10c
|
Simplificar: 8x + 4z -12 + 6x - 10z
+ 4
Procedimiento:
8x + 4z -12 + 6x -
10z + 4 = (8
+ 6)x + (4 - 10)z + (-12
+ 4)
Se hace de forma similar al caso anterior (cuidado con
las operaciones con los números enteros), la simplificación
queda:
8x + 4z -12 + 6x - 10z + 4 = 14x - 6z
- 8
|
En todos los casos de este apartado se puede notar en el paso
intermedio la aplicación de la ley distributiva en el
siguiente sentido:
ba +
ca = (b
+ c)a
3.4. Otros casos de simplificación
Simplificar: 5(a + 2b) + 7b
Procedimiento:
Primero se aplica la ley distributiva: 5(a
+ 2b) + 7b = 5a + 10b +
7b
Ahora se reducen los términos semejantes: 5a
+ 10b + 7b =
5a + (10 + 7)b = 5a + 17b
Por lo que la simplificación queda así:
5(a + 2b) + 7b = 5a + 17b
|
Simplificar: -4(8x + 12y) - 4x + 6y
Procedimiento:
Primero se aplica la ley distributiva: -4(8x
+ 12b) - 4x + 6y = -32x
- 48y - 4x + 6y
Ahora se reducen los términos semejantes: -32x -
48y - 4x + 6y = -36x +
42y
Por lo que la simplificación queda así:
5(a + 2b) + 7b = 5a + 17b
|
| Operaciones Algebraicas |
|
Polinomio es una expresión algebraica formada
por términos que son productos de variables y
números o solamente por números y variables,
términos relacionados entre si por las operaciones
de suma y resta y sin variables en el denominador de
ninguno de ellos.
Son polinomios:
5x² + 2x - 7
|
2y - 3x + 5
|
-8 + a³ - 6a + 11a²
|
No son polinomios:
Cuando una de estas expresiones tiene un único
término se llama monomio, cuando tiene dos téminos
recibe el nombre de binomio y con tres términos
es trinomio.
| Monomios: |
5
|
-3x
|
9as³
|
| Binomios: |
b + 4x
|
4y - 12y³
|
6wV - 7
|
| Trinomios: |
3 - x + x²
|
7abc +4ac - b
|
-6s +13 + 2sx
|
Para sumar polinomios
- Se ordenan los polinomios
- Se escriben los polinomios, uno debajo de
otro (cada polinomio en una fila diferente),
de tal forma, que los términos semejantes
queden en la misma columna
- Se reducen los términos semejantes
- Se dibuja una línea debajo de la última
fila; y debajo de esta línea se escriben
los términos, ya reducidos en el paso
3, con sus respectivos signos.
|
Ejemplo 1:
| Sumar dos polinomios: |
|
Procedimiento según
los cuatro puntos anteriores: |
|
| Suma: |
|
Nota: Se recuerda que cuando el coeficiente es 1 o -1,
no se escriben. En los polinomios del ejemplo c es 1c y -c es -1c
Ejemplo 2:
| Sumar tres polinomios: |
|
| Procedimiento: |
|
| Suma: |
|
Ejercicios: Para cada renglón efectuar la sumas de los polinomios
dados.
Para restar polinomios
- Se identifican tanto el minuendo como sustraendo
- Se escribe el minuendo con su propio signo y a continuación
el sustraendo con signo cambiado. O también, el minuendo
en una fila y en la fila inferior el sustraendo, cada término
con el signo cambiado y cada término en la misma columna
que su semejante.
- Se reduce la expresión resultante.
Se llama minuendo a la cantidad de la que se resta otra cantidad.
El sustraendo es la cantidad que se resta.
|
En el subtema Enteros (Ver
el mapa conceptual) la operación de resta se define
por medio de la operación de suma: a
- b = a + (-b), los siguientes casos lo ejemplifican:
-5
- 2 = -5 + (-2). En la práctica
el sustraendo cambia de signo.
7
- (-4) = 7 + (-(-4)) = 7
+ (4). Cambia de signo el sustraendo,
pasó de -4 a 4.
Esta definición es la que explica el punto dos del procedimiento
para restar polinomios.
Ejemplo 1:
| Restar los polinomios: |
|
Procedimiento según
los tres puntos anteriores:
|
El minuendo es: 3a + 2b
El sustraendo es: 2a - 3b
La resta se define como suma, cambian los signos del sustraendo:
3a + 2b - (2a - 3b) = 3a + 2b + (-2a + 3b)
Se elimina el paréntesis y se reducen términos
semejantes:
3a + 2b + (-2a + 3b) = 3a + 2b - 2a + 3b = a +5b
|
| Resta: |
3a + 2b - (2a - 3b) = a + 5b
|
Ejemplo 2:
| Restar los polinomios: |
2x -3y menos
-x + 2y
|
| Procedimiento: |
El minuendo es: 2x -3y
El sustraendo es: -x + 2y
La resta se define como suma, cambian los signos del sustraendo:
2x -3y - (-x + 2y) = 2x -3y + (x - 2y)
Se elimina el paréntesis y se reducen términos
semejantes:
2x -3y + (x - 2y) = 2x - 3y +x - 2y = 3x - 5
|
| Resta: |
2x -3y - (-x
+ 2y) = 3x - 5y
|
Ejercicios: Para cada renglón efectuar la resta de los polinomios
dados.
| 6. Multiplicación de polinomios |
|
Para multiplicar monomios
- Se multiplican los coeficientes numéricos incluyendo
sus signos aplicando las leyes de los signos.
- Se multiplica la parte literal aplicando la siguiente ley
del producto de potencias: "para multiplicar potencias
de la misma base, se escribe la base común y se eleva
a un exponente igual a la suma de los exponentes de los factores"
|
Ejemplo 1:
Multiplicar dos monomios
|
|
Procedimiento según
los tres puntos anteriores y resultado. |
El producto de dos números con
el mismo signo es un número positivo. Esto se usa al multiplicar
-4 por -5, el signo positivo en general no se escribe.
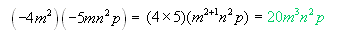
|
Ejemplo 2:
| Multiplicar |
|
| Procedimiento resultado: |
El producto de dos números con signo diferente
es un número negativo. Esto se usa al multiplicar 5 por
-6, el signo es negativo.
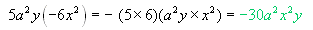
|
Para multiplicar monomios por polinomios
- Se multiplica el monomio por cada uno de los términos
del polinomio, en el siguiente orden:
a. se multiplican los
coeficientes entre si, teniendo presente
la "Ley de los signos"
b. se multiplica la
parte literal. Cada letra particular
representa una base; "el producto
de varias potencias con igual base se
obtiene escribiendo la base común
y sumando los exponentes respectivos.
- Se ordena el polinomio resultante
|
Ejemplo 1:
Multiplicar
|
|
| Procedimiento según los dos puntos anteriores y resultado. |
|
Ejemplo 2:
| Multiplicar: |
|
Procedimiento y resultado:
|
|
Ejercicios: Para cada renglón efectuar la multiplicación
de los polinomios dados.
Ejercicios para hacer en
el cuaderno
|
|
|
1.
|
Evaluar
- 5xy cuando x= - 3, y = 4
|
|
2.
|
Evaluar
3(x² + 1) donde x = - 5
|
|
3.
|
Multiplicar
- 4(2x - 6)
|
|
4.
|
Multiplicar
2(x - y)
|
|
5.
|
Reducir
términos semejantes: 8x - 5x
|
|
6.
|
Reducir
términos semejantes: -3x + 2 -5y - 6x + 8
|
|
7.
|
Reducir
términos semejantes: 5(x - 3) + 7x -8
|
|
8.
|
Reducir
términos semejantes: -5a + 2b - 7c + 6c - 3b +3a
|
|
9.
|
Reducir
términos semejantes: 7(3x - 8) + 2(x - 5)
|
|
10.
|
Encontrar
la temperatura en grados Celsius ( °C) cuando la temperatura
en grados Fahrenheit es de 86°. Use C = 5/9(F
- 32)
|
Ir al inicio
|
|





